Call With Current Continuation

This post is part of the blogpost series explaining coroutines, how they implemented in various programming languages and how they can make your life better:

“Call with current continuation” (abbreviated as call/cc) originates in Scheme. It’s not as widespread as yield/async/await and less intuitive than coroutines as threads implementation. On the other hand, it seems to be quite influential because Scheme was one of the first high-level languages to have coroutines and continuations. Because call/cc comes from Scheme all code examples in this post are written in Scheme (and should be executable with CHICKEN Scheme).

Before diving into calcc, it’s worth understanding what continuation is or rather what people mean when they say “continuation”. There are several meanings:

A callback passed into a function. In other words, if a function takes another function as an argument and calls it at some point, the argument is “continuation”.
A function representing the rest of a program. This is a bit more academic definition in which “the rest of the program” actually means the rest of the program, e.g. if we transform a program to extract all the code after the current expression into some function, that function will be “continuation”.
Representation of a continuation in a particular programming language (e.g. as a class or an interface).
Compiler or VM support for continuations.

Continuation-passing style

Continuation-passing style (abbreviated as CPS; not to be confused with CSP) is a way to structure programs so that all functions take an additional argument called continuation and instead of finishing or returning, functions invoke the continuation. For example, the program below is “hello world” written in direct style. It uses the built-in display function to print messages.

(define (main args)
  (display "hello ")
  (display "world")
)

The same program rewritten in CPS with custom display-cps function might look like this:

(define (display-cps message continuation)
  (display message)
  (continuation)
) 
(define (main args)
  (display-cps "hello " (lambda ()
    (display-cps "world" (lambda () #f))
  ))
)

As you can see the main function has changed quite a bit. Instead of two statements invoking display it’s now a single statement calling display-cps which takes an anonymous function as an argument. The anonymous function created with (lambda () ... ) contains the second statement with a call to display-cps. The last lambda is no-op and returns #f (“false” in Scheme) simply because it has to return something.

Identity function, which unlike “hello world” has a return value, is another trivial example showing the difference between direct style and CPS. It’s worth noticing that continuation is used here almost like the return keyword in imperative languages.

(define (identity value)
	value
)
(define (identity-cps value continuation)
	(continuation value)
)
(define (main args)
	(display (identity 42))
	(identity-cps 42 (lambda (value)
		(display value)
	))
) 

Here is another less trivial example of converting recursive factorial implementation to CPS. Factorial written in direct style might look something like this:

(define (factorial n)
	(if (= n 0) 1
	(* n (factorial (- n 1))))
) 
(define (main args)
	(display (factorial 5))
)

The same program rewritten in CPS:

(define (factorial-cps n continuation)
	(if (= n 0) (continuation 1)
	(factorial-cps (- n 1) (lambda (result)
		(continuation (* n result))
	)))
) 
(define (main args)
	(factorial-cps 5 (lambda (result)
		(display result)
	))
)

To convert the factorial function to CPS we add one more argument to factorial-cps and use it almost like a return statement. This is straightforward for values, e.g. in (continuation 1). However, it’s a bit more subtle when calling other functions, e.g. (continuation (* n (factorial-cps (- n 1))))) won’t work. The problem is that the result of factorial-cps is only accessible in its callback, so we need to invoke continuation inside the lambda. Similarly, in the main function we display result by passing callback (aka continuation) to factorial-cps.

Here is another example of CPS in which we read a file from web server, save it into a file and open the file with default application. Hopefully, this is somewhat convincing that any program can be rewritten in continuation-passing style. However, as you can see in the main function, the code quickly becomes very nested. This is callback hell (aka pyramid of doom) and this is when call/cc can be really useful.

(use http-client)

(define (read-from-url url continuation)
	(continuation (with-input-from-request url #f read-string))
) 
(define (save-to-file path data continuation)
	(with-output-to-file path (lambda () (display data)))
	(continuation path)
) 
(define (open-file path continuation)
	(system (string-append "open " path))
	(continuation path)
) 
(define (main args)
	(read-from-url "http://i.pinimg.com/736x/35/f7/83/35f783f18d40b7d41fae5c51a25709d1.jpg" (lambda (data)
		(save-to-file "src/3-coroutines-as-callcc/0-cps/scheme/no-cat.jpg" data (lambda (path)
			(open-file path (lambda (path)
				(display (string-append "Opened: " path))
			))
		))
	))
)

(Strictly speaking, this example and examples before could be broken down further, e.g. re-writing if, =, -, *, display, string-append in CPS.)

Basic call/cc

Below is a basic example of using call/cc (“/cc” stands for “with current continuation” where “/” is part of the function name just like any other character).

(define (print message)
    (display message)
    (newline)
)
(define (main args)
    (print 1)
    (print (call/cc (lambda (continuation)
        (print 2)
        (continuation 3)
        (print "🙈")
    )))
    (print 4)
) 

As you might expect the output is:

After printing 1 the program invokes call/cc which takes lambda as an argument. The lambda is evaluated straight away and prints 2. Then (continuation 3) is called and this is where things become more interesting. Calling continuation will finish execution of the call/cc expression evaluating it to the value passed to continuation. In the example below it’s equivalent to replacing (print (call/cc ... )) with (print 3). The rest of the code in the lambda will not be executed so it will never print 🙈. As in the previous examples continuation represents the rest of our program except that with call/cc we didn’t have to make any effort to write code in continuation-passing style and got current continuation without restructuring code.

Rocket jump

Previously we used continuation inside the callback. But there are other options, e.g. saving reference to continuation and invoking it later outside of the callback several times. This is exactly what the following example is about.

(define (print message)
    (display message)
    (newline)
)
(define (main args)
    (define count 0)

    (print (+ 100 (call/cc (lambda (continuation)
        (set! saved-continuation continuation)
        (continuation 100)
        (print "🙈")
    ))))

    (if (< count 3) (begin
        (set! count (+ 1 count))
        (print "🚀")
        (saved-continuation count)
    ))
)

The program will print:

The main difference here is that in call/cc callback continuation is saved into a global variable saved-continuation. Then we “return” from the callback with (continuation 100) so the print statement becomes (print (+ 100 100)) and will print 200. Later on after printing 🚀, we invoke (saved-continuation count) so the program jumps back to the expression where call/cc was initially invoked and evaluates call/cc expression to the current value of count. Effectively, this is transferring control flow right into the middle of + expression, something that can’t be easily done in most programming languages. It’s repeated while counter is less than 3, otherwise, the program would loop forever.

The following diagram illustrates the example using notation from the previous blogpost. Similar to coroutines as threads and yield/async/await, you can think about continuation as saving the current stack and instruction pointer somewhere in memory and using it later to return to a particular point in the program. Overall, this is how coroutine implementations and continuations are related to each other.

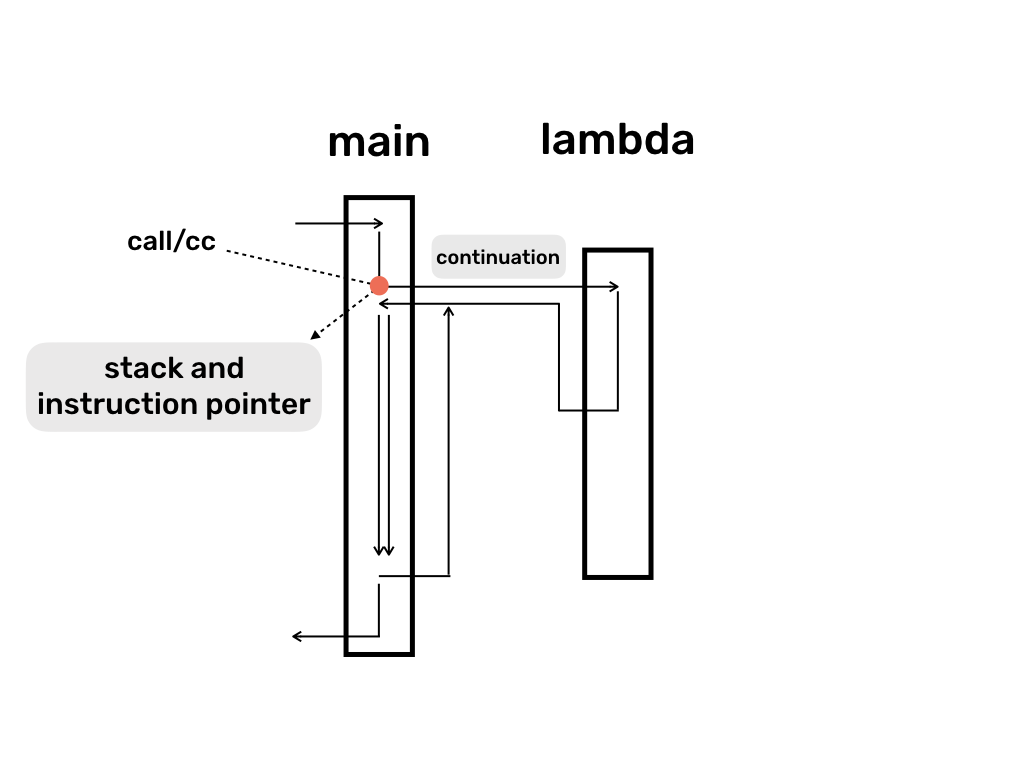
Yield with continuations

Continuation is a more fundamental concept than coroutine and, therefore, can be used to implement coroutines and other control structures such as exceptions. The following example shows minimal implementation of yeild/resume using call/cc. The main idea is the same as in the rocket jump example. We save the current continuation into a variable (in this case yield-point and jump-out) and use it later to change execution flow. For simplicity, this example uses global variables, but they could be scoped within some object with yield and resume functions so it will look more like a normal generator.

(define (print message)
    (display message)
    (newline)
)

(define (make-generator callback)
    (define (yield)
        (call/cc (lambda (continuation)
            (set! yield-point continuation)
            (jump-out #f)
        )))
    (define (resume)
        (call/cc (lambda (continuation)
            (set! jump-out continuation)
            (yield-point #f)
        )))
    (define yield-point #f)
    (set! yield-point (lambda (_)
        (callback yield)
        (jump-out #f)
    ))
    resume
)

(define (f yield)
    (print 2)
    (yield)
    (print 4)
    (yield)
    (print 6)
)

(define (main args)
    (print 1)
    (define resume (make-generator f))
    (resume)
    (print 3)
    (resume)
    (print 5)
    (resume)
    (print 7)
)

Summary

It might seem that continuations are just implementation details of a particular compiler/interpreter. But there is more to them than just a compiler feature. Continuations are a fundamental concept and naturally come up in computer science. For example, in the Definitional Interpreters for Higher-Order Programming Languages paper by John Reynholds which you can watch being explained by Philip Wadler at the Papers We Love meetup.